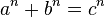viernes, 21 de octubre de 2011
el blog
blog creado para el profesor de matematicas esta actividad la realizo constanza vigeras y valerie ross del 3ªa
filantropia
La etimología de la palabra filantropía deriva sus raíces del griego φίλος philos (o filos), y άνθρωπος, anthropos, que se traducen respectivamente como 'amor' (o 'amante de', 'amigo de'), y 'antropos' (o 'ser humano'), por lo que filantropía significa 'amor a la humanidad'. Su antónimo es misantropía.
En general, la filantropía significa el amor al género humano y todo lo que a la humanidad respecta, particularmente, en su forma positiva y constructiva, expresado en la ayuda a los demás sin que necesariamente se requiera de un intercambio o interés alguno en una respuesta.
Los esfuerzos filantrópicos son realizados por parte de individuos o por grupos de individuos organizados.
Los donativos a organizaciones humanitarias, personas, comunidades, o trabajando para ayudar a los demás, directamente o a través de organizaciones no gubernamentales con fines no lucrativos, así como lo es el trabajo de voluntario para apoyar instituciones que tienen el propósito específico de ayudar a los seres vivos y mejorar sus vidas, son considerados actos filantrópicos, siempre y cuando no estén movidos por intereses.
tríos pitagóricos
Tríos Pitagóricos - Ejemplos
Tríos (Números) Pitagóricos:
Un trío de números enteros positivos (a,b,c) se dice que son números pitagóricos sí y sólo sí satisfacen la siguiente ecuación:

Estos números sirven para construir triángulos rectángulos, donde el mayor es la hipotenusa y los dos menores los catetos.
Ejemplos:

demostracion de wiles
Último teorema de Fermat establece que no existe solución con números enteros no nulos para la ecuación: xn + yn = zn si n es un entero más grande que dos.
| Asociación entre Fermat y Taniyama |
| Si p es un primo impar y a, b y c son enteros positivos tales que ap+bp=cpentonces la ecuación correspondiente y² = x(x - ap)(x + bp) define una curva elíptica hipotética, llamada la curva de Frey, que debe existir si hay un contraejemplo al último teorema de Fermat. Siguiendo el trabajo de Yves Hellegouarch, quien fue el primero en considerar esta curva, Freyseñaló que si tal curva existiese tendría propiedades peculiares, y sugirió en particular que aquella curva no sería unacurva modular. |
Teorema de fermat
En teoría de números, el último teorema de Fermat, o teorema de Fermat-Wiles, es uno de los teoremas más famosos en la historia de la matemática. Utilizando la notación moderna, se puede enunciar de la siguiente manera:
|
El teorema fue conjeturado por Pierre de Fermat en 1637, pero no fue demostrado hasta 1995 por Andrew Wiles ayudado por Richard Taylor. La búsqueda de una demostración estimuló el desarrollo de la teoría algebraica de números en el siglo XIX y la demostración del teorema de la modularidad en el siglo XX.
Suscribirse a:
Entradas (Atom)